And I'll compress and decompress your data without losing any integrity! ... Okay, so maybe this programme isn't the "Big Bad Wolf," and it certainly won't be blowing down any houses, but lossless data compression is still a very very important thing (just don't try entertaining children with it — I mean really, I don't know where I was going with that joke). In any case, I recently did a lot of reading on lossless compression algorithms and decided I wanted to try implementing one; enter Huffman Coding.
What the heck is Huffman Coding?
David A. Huffman was a computer scientist specialising in information theory who basically changed the world with the invention of his de/compression algorithm. The way it works is by assigning smaller bit length codes to more frequently occurring data sequences within a stream, and relatively larger codes to less frequently occurring data sequences. Huffman Coding gave way to a tonne of other compression algorithms, such as the popular DEFLATE, and variations of it are used in popular multimedia formats such as the MP3 codec, and the PNG and JPEG image formats. If implemented correctly, and operating on large enough files, the data savings are usually around 40 to 50%.
Really, the beauty of the algorithm is in its simplicity. Essentially the process is split up into three parts; indexing the frequency of each data sequence in the data stream (for instance a character in a text-file), building a Huffman tree from this index, and generating and writing variable length "prefix-codes" to a new file. The implementation is a bit more complicated than that though.
My implementation consisted of a C++ programme which operated exclusively on text, so from here on out we're only talking about ASCII characters as far as data is concerned.
The Huffing (compression)
Let's imagine that we have a simple text file which contains the following:
aaaabbaacccbcabbaaccda
Here we have 176 bits (22 characters x 8 bytes) of data. A lot of this data is (deliberately, for the sake of
example) repeated though. Here's the frequency breakdown of the characters in the file:
| Char. | a | b | c | d |
|---|---|---|---|---|
| Freq. | 10 | 5 | 6 | 1 |
With this data, a frequency based binary tree is built. This is done by assigning each character-frequency pair to a node and placing them into a priority queue. The nodes are combined sequentially, de-queuing the two nodes with the smallest frequencies, combining them, and adding them back into the queue. This de-queuing, combining, and re-queuing the nodes repeats until only one remains.
Using this example, the nodes d-1 and b-5 should be combined first. To do this, a
new root node needs to be created with a null character and a frequency value equal to the sum of both of it's
childrens' (d-1 and b-5) frequencies. The resultant tree could be represented like
this:
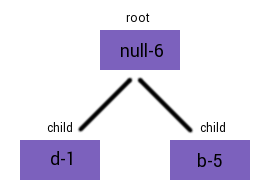
Following this, the nodes null-6 and c-6 should be combined to make
null-12. null-12 and a-10 then get combined to make the final Huffman
tree. It's from this tree that we generate the "prefix-codes".
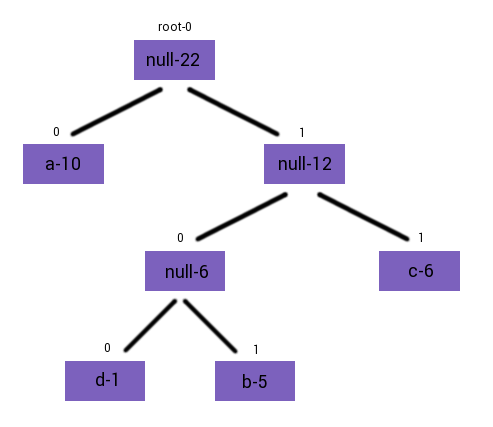
To generate the prefix codes for each letter, all we do is recursively trace the tree until we end up at a valid character. Every time we go left, we append a zero to the code, and every time we go right, we append a one. Simple.
What do we do with these prefix codes though? We use them to "flatten" the tree, writing one of each unique character prepended by the prefix codes to a binary file. The flattened tree (traversing leftmost-deep to rightmost-deep) for this example might look like:
0 97 100 100 101 98 11 99
Where every other integer is the ASCII encoding for a particular character. Decompression is simply a matter of parsing the integers from the binary file to reconstruct the Huffman tree. Performing an analysis on the tree will then yield the original text that was compressed.